小サンプルの分割表に対するフィッシャーの正確検定の使用

この記事の執筆者は ポール・リッチコラボツリーのエキスパートであるのコラムに掲載されたものです。 データ・ドリブン・ジャーナリズム.

この記事では、小サンプルの分割表にフィッシャーの正確検定をどのように使用できるかを概説します。における共通の問題は データ分析 は，性別，人種，選挙での2人の候補者の得票率など，2つのカテゴリー変数の間に統計的な関係があるかどうかを判断する方法です。 関係を視覚化する最も簡単な方法は、2つの変数の各組み合わせのカウントを、行が一方の変数のレベル、列が他方の変数のレベルを表す分割表で表すことです。 行と列の変数の間に関連性があるかどうかを調べる最も一般的な統計的検定は、カイ二乗（χ²)のテストを行います。 下の表の例は、このテストを説明するために与えられたものです。

	民主党の勝者（コラムの%		合計
	クリントン勝利	サンダース勝利
トランプ1st	25 (86%)	12 (55%)	37
トランプ2位	3 (11%)	8 (36%)	11
トランプ3位	1 (3%)	2 (9%)	3
合計	29 (100%)	22 (100%)	51

上の表の列は、民主党側のヒラリー・クリントンとバーニー・サンダースが獲得した主要州と、共和党側のドナルド・トランプが同じ主要州に配置された州を示しています。コロンビア特別区を含むため、表中の州の数は51です。列のパーセンテージを見ると、トランプ氏はクリントン氏が獲得した主要州のうち86%を獲得したのに対し、サンダース氏が獲得した州のうち55%を獲得しました。

カイ二乗検定では、表の各セルの期待値を計算します。例えば、共和党でトランプ氏が3位になった州と、民主党でバーニー・サンダース氏が勝利した州のセルの期待値（変数間に関係がない場合に期待されるセルの値）は、トランプ氏が3位になった州の行の合計（3）に、サンダース氏が勝利した州の列の合計（22）を掛けることで計算されます。そして、この積をオブザベーションの総数（51）で割ります。期待値の計算式は次のように与えられます。

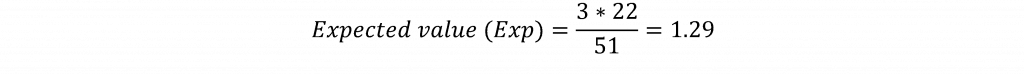
つまり、このセルは、トランプ氏が3位、サンダース氏が勝利した主要州が互いに完全に独立していた場合、1.29という値が予想されます。 このセルの観測値は2で、このセルの数が予想よりも多いことを示唆しています。 期待値は表の各セルについて計算され、各セルの観察値と期待値の差が計算され、二乗され、期待値で割られ、式に従って表の各セルに合計されます。

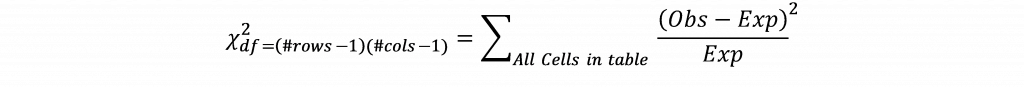
カイ二乗の値が、与えられた自由度（行数マイナス1、列数マイナス1を掛け合わせて求められる）とp値に対するカイ二乗臨界値を超えた場合、変数間に関連性があると判断されます。

カイ二乗検定には問題があります。 これは、分割表における計数の分布の近似です。 表のセルのうち20%以上が5未満の期待値を持つ場合、行変数と列変数の間の関連性の仮説を検定するのに、カイ二乗近似は機能しません（下の表のように）。 この表の変数はどちらもカテゴリー変数です。 主要な統計パッケージは、この仮定に違反した場合、ユーザーに警告します。 この仮定に違反すると、観測されたp値が不正確になり、関連性の有無に関して誤った結論を出すことになります。 カイ二乗検定に代わる正確な検定として、フィッシャーの正確検定があります。

フィッシャーの正確検定は、超幾何学的確率分布に基づいています。

ここでは、その R_i! は、行の合計値の階乗（5！＝5*4*3*2*1）です。 C_i! は各列の合計値の階乗です。 N! は表の合計の階乗であり、ア_ij!"は個々のセル値の階乗です。 Π_ij is the product coefficient of the individual cell values.  Such a formula is even more computationally intensive than the chi-square test, especially for tables with many rows and columns.  This is why the chi-square test was favored in the past because it took too much memory for computers to run.  These days it is less of an issue for computers to run the Fisher’s exact test and it is easy to run in the major statistical packages (R, SAS, SPSS, スタタ, etc.).

R（無料のプログラム）でフィッシャーの正確検定とカイ二乗検定を行うコマンドは、記事の上部にある表と対応する出力（フィッシャーの正確検定は黄色、カイ二乗検定は緑色）について、以下で見ることができます。

 

 

 

 

 

 

 

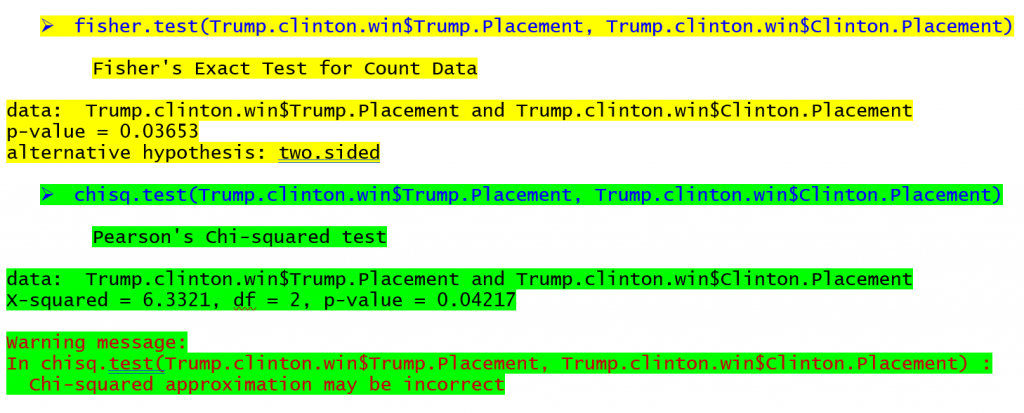
フィッシャーの正確検定の出力では、行と列の間に関連性がない場合、これらの表の頻度を観察する確率が0.03653であることが示されています。 カイ二乗検定の出力では、同じ表に関連性がある場合、0.04217の確率であることがわかります。 有意性の基準として.05のp値を使用していた場合、p値は異なりますが、このケースでは両方の検定で関係があることがわかります。 予備選挙でヒラリー・クリントンが勝利した州は、ドナルド・トランプが勝利する可能性が高く、バーニー・サンダースが勝利した州は、トランプが2位になる可能性が高かった。^nd または3^rd サンプルサイズがさらに小さい表では、p値の差がさらに大きくなり、結論が大きく異なってしまう可能性があります。

警告として、p値はカテゴリー変数間の関連の強さの指標として使用してはいけません。 検定が有意であるか否か。 p-値はサンプルサイズに敏感です。 多くの場合，効果量を推定するためにオッズ比が使用されますが，Rでは2列2行の表を対象としたfisher.test関数でのみ計算されます．

フィッシャーの正確検定は、サンプル中の2つのカテゴリー変数の間で観察されたパーセンテージの違いが、有意であるか、それとも単にデータのランダムなノイズによるものかを判断する基準を提供します。 上の例では、クリントンとトランプが獲得したプライマリー・ステートの86%は、サンダースとトランプが獲得したプライマリー・ステートの55%と有意に異なっています。 ジャーナリストは、観測されたパーセンテージやカウントを見ただけでこのような判断をすることは、主観的なものであるため、常に注意が必要です。 主観的な判断は、データに関連する問題についての先入観によってさらに曇ってしまう可能性があるからです。