Comment corriger les valeurs aberrantes dans les modèles de régression : Un exemple avec la race, l'éducation et les non-assurés sur le vote de Trump

Ce billet a été initialement publié dans ma chronique sur le site le journalisme basé sur les données.

Dans mon Dans mon dernier billet, j'ai parlé de la façon dont la régression peut être un outil utile pour démêler les différentes relations entre les variables corrélationnelles. J'ai également parlé de la façon dont les valeurs aberrantes peuvent être problématiques. Une façon de traiter une valeur aberrante est de la supprimer purement et simplement de l'analyse. Ce faisant, on diminue la puissance statistique (la probabilité de trouver un prédicteur significatif lorsqu'il existe) et on supprime du modèle des informations potentiellement précieuses. Cette démarche peut s'avérer plus fructueuse, car elle permet d'obtenir des informations précieuses. J'ai fait cela dans mon post sur la façon dont Washington, DC diffère des autres États et cela m'a donné une idée pour une autre covariable qui devrait être prise en compte en plus de celles déjà prises en compte : concentration de groupes haineux, % non assuré, % avec un diplôme de licence ou plus, et % dans la pauvreté.

Dans mon post sur les caractéristiques de Washington, DC en tant qu'aberration J'ai constaté qu'il est le moins blanc de tous les États considérés. Seulement 40,2% de la population du district s'identifie comme blanche ou caucasienne. Seul Hawaii avait un plus petit % blanc avec 25,4%. Dans le sondage de sortie des urnes pour l'élection de l'année dernière, 60% des femmes blanches sans diplôme universitaire ont voté pour Trump, contre 71% des hommes blancs sans diplôme universitaire. 74% des non-Blancs ont voté pour Clinton.

L'ajout de cette variable au modèle a amélioré de manière significative la précision du modèle avec DC inclus, 78,5% de la variabilité du vote de Trump étant pris en compte. Les variables relatives aux groupes haineux et à la pauvreté % n'étaient pas significatives et ont été exclues car leur présence dans le modèle diminue la puissance statistique. Les variables % baccalauréat, % Blanc et % non assuré étaient significatives (ce qui signifie que la valeur p est inférieure à 0,05 - je l'expliquerai dans un prochain article), les autres ne l'étaient pas. La sortie de la plupart des progiciels statistiques :

78.5% de la variabilité comptabilisé	Coefficients	Erreur standard	t Stat	Valeur P	Plus bas 95%	Upper 95%
Intercepter	51.55	8.92	5.78	5.75E-07	33.61	69.48
% bachelor's degree ou plus	-1.11	0.15	-7.55	1.2E-09	-1.41	-0.82
% Blanc	0.31	0.06	4.95	1.01E-05	0.18	0.43
% non assuré	0.74	0.26	2.86	0.006319	0.22	1.26

La colonne intitulée "coefficients" donne les valeurs estimées de l'équation de régression que j'ai expliquée dans les messages précédents. L'équation actuelle est la suivante :

Trump % des voix = 51,55 - 1,11*(% bachelor) + 0,31*(% Blanc) + 0,74*(% Non assuré)

Cela signifie que lorsque toutes les covariables sont égales à zéro, on prédit que Trump aura 51,55% des voix. Pour chaque augmentation de 1% du nombre de bacheliers (%), on estime à 1,11% la diminution du nombre de votes pour Trump. Pour chaque augmentation de 1% de la % de la population blanche dans l'État, il y a une augmentation estimée de 0,31% et pour chaque augmentation de 1% de la % des personnes non assurées dans l'État.

La colonne intitulée "erreur standard" est une estimation de l'incertitude des coefficients. La colonne intitulée "t stat" est la statistique de test permettant de déterminer si les coefficients sont significativement différents de zéro. La "valeur p" est la probabilité estimée d'observer ce coefficient estimé lorsque le vrai coefficient est égal à zéro. Par convention, lorsque la valeur p est inférieure à 0,05, nous concluons que le vrai coefficient est différent de zéro. Les deux dernières colonnes indiquent les limites supérieure et inférieure d'un intervalle de confiance de 95% pour un coefficient. L'intervalle de confiance indique que, 95% du temps où les estimations sont faites, le vrai coefficient se situera entre les limites supérieure et inférieure. Dans ce cas, si les limites supérieures et inférieures ne sont pas à cheval sur le chiffre zéro, cela équivaut à dire que le coefficient est significativement différent de zéro.

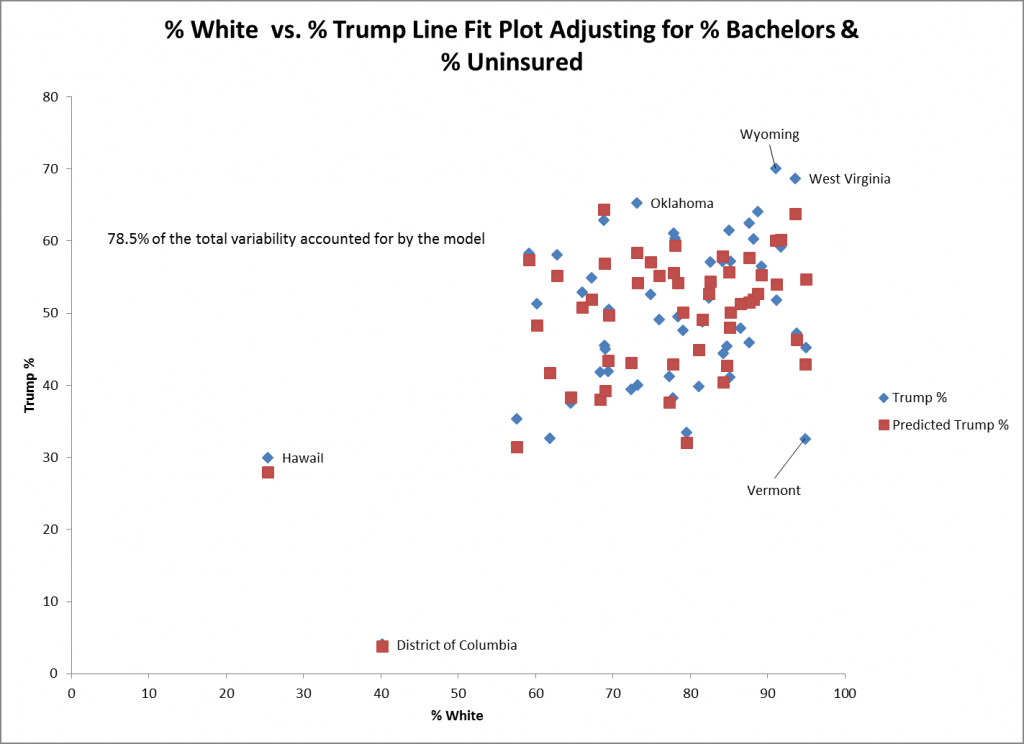
Le nuage de points ci-dessus montre les valeurs réelles (dans le losange bleu) et prédites (dans les carrés rouges) pour % blanc et % Trump pour le modèle ajustant pour % bacheliers et % non assurés. Les valeurs réelles et prédites pour le District de Columbia (DC) et Hawaii sont très proches les unes des autres, ce qui suggère une bonne adéquation. L'État du Vermont est mal ajusté : le vote réel pour Trump est inférieur de 10% au vote prédit, comme on peut le voir directement au-dessus du diamant bleu pour le Vermont.

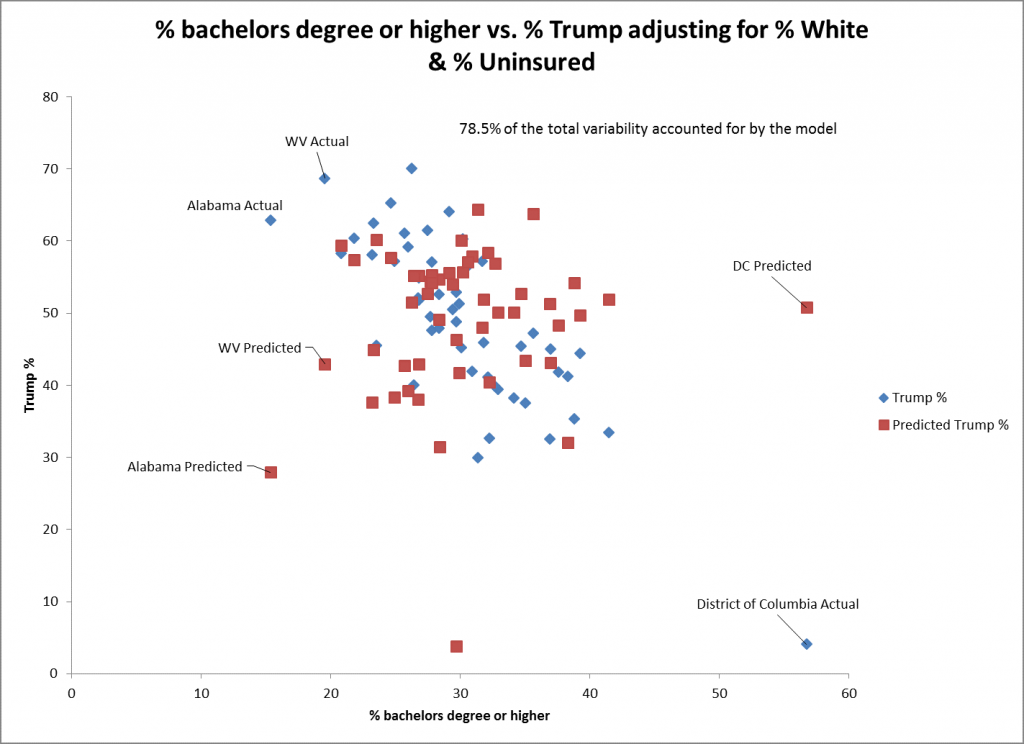
Le diagramme de dispersion pour % baccalauréat ou plus suggère que l'ajustement n'est pas aussi bon que pour celui pour % blanc comme prédicteur. Cela se reflète dans l'erreur standard plus grande pour ce prédicteur (0,15) que pour % blanche (0,06). La prédiction pour DC n'est pas aussi bonne pour ce prédicteur, car elle est la plus élevée. La tendance est toujours significative dans la direction négative.

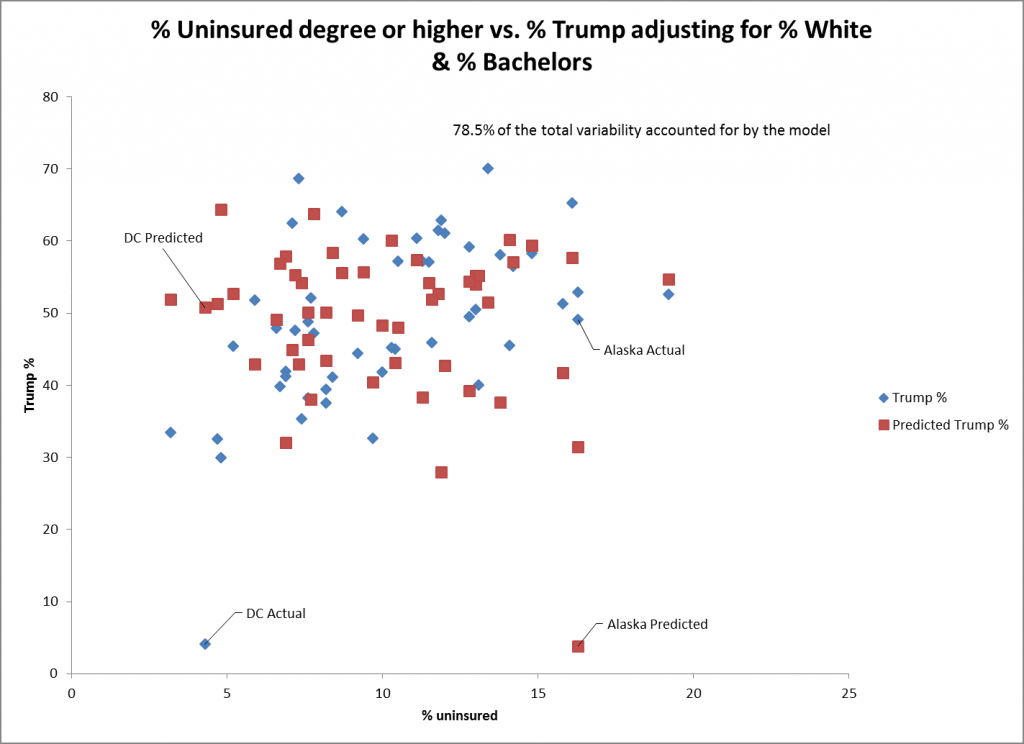
Le nuage de points pour % non assuré comme prédicteur montre encore moins d'adéquation pour % des votes de Trump. Le DC et l'Alaska sont des points mal ajustés pour ce prédicteur parmi de nombreux autres États. L'erreur standard pour ce prédicteur montre un ajustement encore plus faible (0,26) pour les autres prédicteurs, bien qu'il soit encore statistiquement significatif.

La régression multiple est un outil potentiellement puissant pour démêler les relations entre les variables prédictives d'un résultat spécifique lorsqu'elle est menée correctement. L'ajout de covariables appropriées, telles que la race, peut contribuer à atténuer les effets d'une valeur aberrante telle que Washington, DC. Il est toujours préférable d'inclure toutes les données afin d'en donner une image aussi complète que possible.

Nous voyons maintenant que plus le % de la population d'un état ayant un diplôme de baccalauréat ou plus augmente, plus le % du vote pour Trump diminue. Dans le même temps, lorsque les pourcentages de blancs et de personnes non assurées dans un État, augmentent, le % du vote pour Trump augmente. En présence de ces variables, la concentration de groupes haineux et le % de l'État en matière de pauvreté ne sont plus des prédicteurs significatifs du vote pour Trump.

Alors que Trump et le congrès contrôlé par les républicains se préparent à abroger la loi sur les soins abordables (ACA ou comme le dit le GOP Obamacare), le Congressional Budget Office estime que 23 millions d'Américains perdront leur assurance maladie dans la version de la Chambre des représentants et une estimation de 22 millions dans la version du Sénat. Dans ce modèle, le taux de non-assurés dans chaque État est positivement corrélé avec le vote de Trump. Trump croit-il que l'augmentation du taux de non-assurés augmentera sa part du vote en 2020 ?

La pauvreté n'a pas été associée au vote de Trump en 2016. La diminution des estimations du nombre de non-assurés depuis l'entrée en vigueur de l'ACA en 2014 est principalement due à l'expansion de Medicaid pour les personnes les plus pauvres et aux subventions qui permettent aux personnes à faible revenu d'acheter une assurance maladie. L'augmentation du nombre de non-assurés pourrait ne pas diminuer le vote de Trump, mais il est peu probable qu'elle l'augmente.